Ingresa a cualquiera de nuestras secciones locas haciendo clic en los siguientes enlaces o en las imágenes respectivas:
RETOS MATEMÁTICOS - WWW.RETOMANIA.BLOGSPOT.COM
Retos con alto contenido pedagógico
RETOS MATEMÁTICOS - WWW.RETOMANIA.BLOGSPOT.COM
La matemática integrada con el juego.
RETOS MATEMÁTICOS - WWW.RETOMANIA.BLOGSPOT.COM
Una manera diferente de ver la matemática.
RETOS MATEMÁTICOS - WWW.RETOMANIA.BLOGSPOT.COM
La integralidad en la matemática.
RETOS MATEMÁTICOS - WWW.RETOMANIA.BLOGSPOT.COM
Retos para pensar
Mostrando entradas con la etiqueta Curiosidades matemáticas. Mostrar todas las entradas
Mostrando entradas con la etiqueta Curiosidades matemáticas. Mostrar todas las entradas
MATELOCAS
RETOS MATEMÁTICOSAlfamética, Alfaméticas Locas, Curiosidades matemáticas, Machetazos matemáticos, Matelocas, Matemáticas divertidas, Matemáticas Locas, Paradojas matemáticas
No hay comentarios

Esta sección Matemáticas Locas o simplemente matelocas la vamos a dedicar a mostrar la matemática de una manera loca, incluiremos muchas de las paradojas matemáticas o falacias, también alfaméticas locas, de igual manera algunas curiosidades matemáticas bien disparatadas que nos pondrán la cabeza grande.
Ingresa a cualquiera de nuestras secciones locas haciendo clic en los siguientes enlaces o en las imágenes respectivas:
Ingresa a cualquiera de nuestras secciones locas haciendo clic en los siguientes enlaces o en las imágenes respectivas:
ALFAMÉTICAS LOCAS
RETOS MATEMÁTICOSAlfaméticas Locas, Curiosidades matemáticas, Matemáticas divertidas, Matemáticas Locas
1 comentario

ALFAMÉTICA 1
Que tal si le decimos a nuestros amigos o al profesor de matemáticas que 2+2=3, imagínense la carota que pondrá, verdad, pues bien, mostrémosle que es "cierto", a través de un problema matemático relacionado con la alfamética, en el que se debe hallar el valor correspondiente a cada letra. Si hay letras repetidas como en este caso, el valor es el mismo.
Al tratar de dar solución a este problema observamos que:
El valor de T es uno, porque por grande que sea el valor de D, la suma nunca será mayor de 20.
- El valor de S, es cero, el único número que nos sirve, S+S debe dar S nuevamente
- Ahora los posibles valores para D tienen que ser mayores o iguales que 5. Es claro que el valor de 5 no sirve, porque obtendríamos al sumar 10 y el cero ya le corresponde a S, y si llevamos 1, nos daría 11 y el 1 le corresponde a T, por lo tanto podemos probar cómo valor para D el 6, sin llevar y al buscar el valor de la letra O, no podemos usar ni el cero, ni 1 ni tampoco el 2, si probamos con 3 la suma nos daría 6, por lo tanto el valor de O es 4. Y así tendríamos resuelta esta alfamética loca.
Ahora te toca a tí, encontrar otras soluciones a esta alfamética loca.
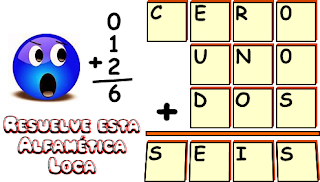
ALFAMÉTICA 2
CERO+UNO+DOS=SEIS. Ahora si que las matemáticas se enloquecieron. Sorprende a tus amigos con este problema alfamético, recuerda las reglas:
- A cada letra le corresponde un único número, un valor entre 0 y 9.
- Letras repetidas, números iguales y letras diferentes, números diferentes.
- Al formar el número de cada palabra, éste no inicia con cero.
Algunas soluciones que nuestro equipo de trabajo encontró son las siguientes.
Sigue buscando y si encuentras otras soluciones hazla llegar a nuestro correo electrónico: retomania@gmail.com con gusto la publicaremos o coméntala a través de este blog.
ALFAMÉTICA 3
A todos nos enseñaron que 1x7=7 sin embargo con este problema matemáticos vamos a mostrar que 1x7=9. Si, así como lo ves, sólo tienes que resolver esta alfamética:
Encuentra a esta alfamética dos soluciones, el menor y mayor producto posible.
ALFAMÉTICA 4
Si las restas fueran así de fáciles, otro gallo cantaría. Atrévete y resuelve esta alfamética loca:
Encuentra el dígito correspondiente a cada letra y consigna los valores en la siguiente imagen:
ALFAMÉTICA 5
Que cinco por dos es siete. Veamos como esto es posible, así es, sólo tienes que averiguar cuál es el dígito que hay que asignar a cada letra para que el producto de la multiplicación sea el indicado, de tal manera que 5x2=7. Encuentra varias soluciones e incluye entre ellas el menor y mayor producto posible.
ALFAMÉTICA 3
A todos nos enseñaron que 1x7=7 sin embargo con este problema matemáticos vamos a mostrar que 1x7=9. Si, así como lo ves, sólo tienes que resolver esta alfamética:
Encuentra a esta alfamética dos soluciones, el menor y mayor producto posible.
ALFAMÉTICA 4
Si las restas fueran así de fáciles, otro gallo cantaría. Atrévete y resuelve esta alfamética loca:
Encuentra el dígito correspondiente a cada letra y consigna los valores en la siguiente imagen:
ALFAMÉTICA 5
Que cinco por dos es siete. Veamos como esto es posible, así es, sólo tienes que averiguar cuál es el dígito que hay que asignar a cada letra para que el producto de la multiplicación sea el indicado, de tal manera que 5x2=7. Encuentra varias soluciones e incluye entre ellas el menor y mayor producto posible.
FALACIAS MATEMÁTICAS
RETOS MATEMÁTICOSCuriosidades matemáticas, Curiosidades numéricas, Falacias matemáticas, Matelocas, Paradojas
No hay comentarios

Una falacia es un razonamiento no válido o incorrecto pero con la apariencia de razonamiento correcto. Las falacias entran a formar parte de las matemáticas locas, sección en la que estamos mostrando muchas de las curiosidades del mundo matemático. En matemáticas encontramos muchos procesos que nos llevan a contradicciones o a falacias, a pesar de que el proceso parece correcto, a un error un tanto sutil e intencionado que es el que nos lleva a resultados curiosos y contradictorios.
FALACIA MATEMÁTICA 1
Que tal si te decimos que dos es igual a 1. Aunque suene bien descabellado observa el siguiente razonamiento:
Otra manera de llegar al mismo resultado 2=1 es el siguiente.
En el siguiente razonamiento también probamos que 2=1. Analiza con mucha atención y encuentra cuál es el error en su desarrollo.
Una vez más estamos probando que 2=1, utilizando en esta oportunidad las derivadas, veamos:
FALACIA MATEMÁTICA 2
4=2. Sorprende a tus amigos con esta falacia matemática. Claro no les cuentes en dónde está el error. ¿Ya lo sabes?
FALACIA MATEMÁTICA 3
Que 1 = 1, difícil de creer, pero con el siguiente razonamiento lo confirmaras.
FALACIA MATEMÁTICA 4
Mostremos ahora que -2 = 1, confírmalo con el siguiente razonamiento. Y dónde está el error, atrévete a encontrarlo.
FALACIA MATEMÁTICA 5
Que tal si le mostramos a nuestros estudiantes que 64 = 65, cómo se sorprenderán.
La siguiente animación ilustrará mucho más esta falacia: (Tomada de: http://mathblag.wordpress.com/2011/08/28/a-paradoxical-dissection/)
Todo parece que está bien, Se tiene 4 piezas, con ellas se arma un cuadrado de lado 8 y por lo tanto su área es 64, luego con las mismas piezas se arma ahora un rectángulo de lado 13x5 con un área igual a 65, lo que comprueba que 64 = 65. Y entonces dónde esta el error. Si se ampliara la imagen del rectángulo, podríamos alcanzar a ver un estrechísimo espacio en la diagonal cuya área no podía ser más que 1, es decir que con las cuatro piezas no es posible armar el rectángulo.
LA MÁGIA DE LOS NÚMEROS
RETOS MATEMÁTICOSClases de números, Curiosidades, Curiosidades de números, Curiosidades matemáticas, Significado de números
No hay comentarios

LA MAGÍA DE LOS NÚMEROS
(Tomado de la Revista: Muy Interesante - Juegos No. 13)
Los números enteros han ejercido siempre una fuerte influencia sobre el espíritu humano. Dejando atrás el proceso de su creación, el hombre se presenta como un ser racional, lleno de misteriosos elementos, independientes de la mente creadora y hasta investidos de poderes mágicos y religiosos.
Conozcamos el significado oculto de los números:
NÚMERO 0
Tardó en ser reconocido como tal. Determina un punto sobre una recta como el 3, el 1/2, el -5. Los hindúes, inventores del sistema de numeración vigente hoy en todo el mundo culto, designaban el signo 0, como el lugar vacío en la escritura de los números, siendo a su vez, remplazado por sunya, palabra que significaba la condición de vacío de un lugar, o sitio en blanco, pero no "nada".
Los arabes, introductores del sistema en España y Sicilia durante la edad media, tradujeron la palabra sifr, la cual fue latinizada por cefiro, de donde procede cero por contracción.
NÚMERO 1
Para los pitagóricos, que formaban una secta religiosa, así como una especie de gremio de matemáticos, el 1 era lo creado por la excelencia y, por lo tanto lo existente de por sí, la mónada o principio activo, que se opone a la díada o principio pasivo. Para el neoplatónico Plotino el 1 representa la inteligencia universal. El 1 es susceptible de dar origen a cualquier otro número entero y, como consecuencia fraccionario, irracional, etc..
NÚMERO 2
Representaba para los pitagóricos el principio pasivo, aquello que no tiene existencia por sí mismo, lo transitorio y efímero. Se singulariza por ser el único número primo entre los pares.
NÚMERO 3
Representó la estabilidad, los cimientos sobre los que reposan todas las cosas. La trinidad hindú está formada por tres dioses o principios: Brahma, el pasado, principio creador; Vichnú, el presente y principio conservador; y, finalmente, Siva, el futuro destructor. Tal es la Trimurti o trinidad de los hindúes, que era representado por un ser de tres cabezas, la de brahama por una luenga barba, tal vez para sugerir la vejez o pasado; la de Vichnú, se presentó risueña, atrayente y juvenil, y por fin, la de Siva, el destructor, de expresión bárbara y feroz.
Pitágoras que procedía de Samos y había viajado por Oriente antes de establecerse en la Magna Grecia, popularizó en Occidente el prestigio místico del número 3. Así como los hindúes, él también creeía en la transmigración.
NÚMERO 4
Los pitagóricos veían en el número 4, la primera causa, autoengendrada o autógena, el Dios uno y cuádruple - no uno y trino-, el Tetractis o Cuadrinidad, combinación de:
- el éter, principio activo y masculino, llamado también mónada;
- la materia, principio femenino o pasivo, denominado díada, formado de tierra y agua (algo así como el caos);
- el tiempo, compuesto de pasado, presente y porvenir, y por ello denominado tríada;
- la causa universal, principio que todo lo envuelve, todo lo abarca y le impone un destino inexorable.
También parece que representaba para ellos los cuatro elementos: fuego, agua, tierra y aire. Los discípulos de Pitágoras juraban por aquel "que había otorgado a sus almas el Tetractis, fuente o raíz de la naturaleza eterna.
NÚMERO 5
Se halla asociado desde la antigüedad con el polígono de cinco lados o pentágono, en especial con el estrellado, que aparece en ciertas monedas griegas y al que se le atribuye desde hace muchos siglos propiedades mágicas y místicas. Los pitagóricos adoptaron este polígono como el emblema de una secta.
NÚMERO 6
Tiene la propiedad de ser igual a la suma de sus divisores, si se exceptúa él mismo dentro de ellos, o sea,
Divisores propios de 6: 1, 2, 3
Suma de los divisores propios: 1+2+3 = 6
San Agustín subordina en cierto modo la voluntad divina al número 6, y no al revés, pues dice:
"Seis es un número perfecto en sí mismo, y no porque Dios haya creado todas las cosas en seis días; más bien es lo contrario: creo todas las cosas en seis días porque este número es perfecto, y lo seguirá siendo aún cuando la obra de seis días no existiese".
NÚMERO 7
Está muy lejos de ser perfecto, pues por ser un número primo, su único divisor menor que él es 1. Sin embargo, se ha enredado en la imaginación con tal terquedad que el mismo Cicerón ha declarado: "Muy pocas cosas hay que no constituyan el nudo del número siete".
Los siete colores del arco iris, la siete cuerdas de la lira, los siete planetas conocidos de los antiguos a los que están asociados los siete días de la semana, las siete puertas de Tebas, el tributo de siete jóvenes que los atenienses pagaban a Creta hasta que Teseo dio muerte al Minotauro, los siete pecados capitales, las siete colinas de Roma y mochos sietés más, parecen dar razón al célebre tribuno romano.
NÚMERO 8
Representaba para los pitagóricos la igualdad de todos los hombres. Y se dice que Heliogábalo solía invitar a su mesa a 8 calvos, 8 tuertos, 8 cojos y 8 tartamudos, a los que arrojaba a las fieras terminada la comida. De este modo, expresaba el emperador su respeto por la igualdad de los hombres y por las doctrinas pitagóricas.
NÚMERO 6
Tiene la propiedad de ser igual a la suma de sus divisores, si se exceptúa él mismo dentro de ellos, o sea,
Divisores propios de 6: 1, 2, 3
Suma de los divisores propios: 1+2+3 = 6
San Agustín subordina en cierto modo la voluntad divina al número 6, y no al revés, pues dice:
"Seis es un número perfecto en sí mismo, y no porque Dios haya creado todas las cosas en seis días; más bien es lo contrario: creo todas las cosas en seis días porque este número es perfecto, y lo seguirá siendo aún cuando la obra de seis días no existiese".
NÚMERO 7
Está muy lejos de ser perfecto, pues por ser un número primo, su único divisor menor que él es 1. Sin embargo, se ha enredado en la imaginación con tal terquedad que el mismo Cicerón ha declarado: "Muy pocas cosas hay que no constituyan el nudo del número siete".
Los siete colores del arco iris, la siete cuerdas de la lira, los siete planetas conocidos de los antiguos a los que están asociados los siete días de la semana, las siete puertas de Tebas, el tributo de siete jóvenes que los atenienses pagaban a Creta hasta que Teseo dio muerte al Minotauro, los siete pecados capitales, las siete colinas de Roma y mochos sietés más, parecen dar razón al célebre tribuno romano.
NÚMERO 8
Representaba para los pitagóricos la igualdad de todos los hombres. Y se dice que Heliogábalo solía invitar a su mesa a 8 calvos, 8 tuertos, 8 cojos y 8 tartamudos, a los que arrojaba a las fieras terminada la comida. De este modo, expresaba el emperador su respeto por la igualdad de los hombres y por las doctrinas pitagóricas.
NÚMERO 9
La inestabilidad de las fortunas les pareció a los pitagóricos tener mucho que ver con el número 9. En nuestros días nos preocupa el hecho de que sea un cuadrado perfecto; que, por su unidad menor que la base del sistema de numeració usual, las operaciones con números cuyas cifras son 9 se presten a ciertas abreviaciones, y el de que todo número dividido por 9 dé el mismo resultado que la suma de los valores de sus cifras, lo cal sirve de fundamento a la llamada prueba de los nueves.
CURIOSIDADES DEL 142857
RETOS MATEMÁTICOS142857, Curiosidades, Curiosidades de 142857, Curiosidades matemáticas, Curiosidades numéricas
1 comentario

Este número 142857 (ciento cuarenta y dos mil ocho cientos cincuenta y siete) se destaca porque presenta un gran número de curiosidades, veamos algunas:
- Tiene la particularidad que al ser multiplicado por la secuencia de 2 a 6, el producto resultante corresponde a las mismas cifras del número original en otro orden. Por esta razón, este tipo de números se denominan cíclicos.
142857 x 2 = 285714
142857 x 3 = 428571
142857 x 4 = 571428
142857 x 5 = 714285
142857 x 6 = 857142
- Al multiplicarlo por 7, no se cumple la particularidad anterior, pero el resultado es también curioso.
142857 x 7 = 999999
- El 7 tiene una relación especial con el número 142857, se observa en el punto anterior. Este número es la parte periódica de un número que es dividido entre 7, sea cual sea el número, los números que conforman 142857 se repetirán siempre en el mismo orden (periodo), empezando de uno u otro dígito.
1/7 = 0.142857142857142857142857142857 . . . Periodo : 142857
2/7 = 0.285714285714285714285714285714 . . . Periodo : 285714
3/7 = 0.428571428571428571428571428571 . . . Periodo : 428571
4/7 = 0.571428571428571428571428571428 . . . Periodo : 571428
5/7 = 0.714285714285714285714285714285 . . . Periodo : 714285
6/7 = 0.857142857142857142857142857142 . . . Periodo : 857142
- Si se eleva al cuadrado y partimos en dos números la potencia, observa lo curioso de este resultado:
- Si se suman los tres primeros dígitos con los tres últimos, se obtiene otro resultado curioso:
142 + 857 = 999
- Y si se suman los dos primeros dígitos con los dos siguientes y los dos últimos:
14 + 28 + 57 = 99
Fuentes
CURIOSIDADES DEL 153
RETOS MATEMÁTICOSCuriosidades, Curiosidades de 153, Curiosidades de números, Curiosidades matemáticas, Curiosidades numéricas
No hay comentarios

El número 153 presenta propiedades muy curiosas. Veamos algunas:




- La suma de sus dígitos es un cuadrado perfecto.

- Es el menor número que puede ser expresado como la suma de los cubos de sus dígitos.

- Este número es igual a la suma de los factoriales de los cinco primeros números.

- La suma de sus divisores propios es un cuadrado perfecto:

- Puede ser expresado como la suma de todos números enteros del 1 al 17
- Es el decimoséptimo número triangular. Ten presente que un número es triangular si puede recomponerse en la forma de un triángulo equilátero. El primer número triangular es el 1, le sigue el 3. Los números triangulares, junto con otros números figurados, fueron objeto de estudio por Pitágoras y los Pitagóricos, quienes consideraban sagrado el 10 escrito en forma triangular, y al que llamaban trianón.

- Es divisible por la suma de sus dígitos: 153 / (1 + 5 + 3) = 17
- Puede ser expresado como el producto de dos números formados por sus dígitos: 153 = 3 x 51.
- En el Evangelio, según San Juan, Cap. 21, se lee que: Los discípulos no habiendo pescado nada durante la noche se disponían a abandonar la tarea, cuando siguiendo el consejo de Jesús, echaron de nuevo la red. "Simón Pedro subió a la barca y sacó la red a tierra, llena de peces grandes, eran ciento cincuenta y tres y, a pesar de ser tantos la red no se rompió. (San Juan, Cap. 21 Versículo 11). Por esto el número 153 se consideró en la antigüedad como número mágico.
Fuentes
CURIOSIDADES DEL 23
RETOS MATEMÁTICOSCuriosidades, Curiosidades de 23, Curiosidades de números, Curiosidades matemáticas, Curiosidades numéricas
No hay comentarios

Retos Matemáticos les trae algunas de las curiosidades que obstenta el número veintitres 23.
Fuentes:
- 23 está formado por los dos primeros números primos y la suma de éstos también es un número primo, 2 + 3 = 5.
- 23 es la suma de tres números primos consecutivos, 5+7+11= 23
- Es el menor de los números primos, cuya suma de los cuadrados de sus dígitos es también un número primo impar.
- 2^n + 3^n es un número primo para n = 0, 1 y 2. Veamos:
- Si el número e es elevado a la pi, el resultado en su parte entera es 23.
- Es el menor de los números primos cuyo número en reverso es una potencia.
- La suma de sus factoriales, corresponde a una potencia de los dígitos que lo conforman:
- 23 es el menor de los números primos que no es suma de dos números de Ulam. Recordemos que un Número de Ulam es un miembro de una secuencia entera, la cual fue concebida por el matemático polaco Stanislaw Ulam. Los dos primeros terminos de Ulam son 1 y 2, le siguen, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53, 57, 62, 69, 72, 77, 82, 87, 97, 99.
- 23 son las parejas de números primos mayores que 23 que suman 1000, y son: (29,971), (47,953), (53,947), (59,941), (71,929), (89,911), (113,887), (137,863), (173,827). (179,821), (191,809), (227,773), (239,761), (257,743), (347,653), (353,647), (359,641), (383,617), (401,599), (431,569), (443,557), (479,521), (491,509).
- La suma de los primeros 23 números primos es 874 que es múltiplo de 23, observa como 874 = 23 x 38 .
- Los problemas de Hilbert conforman una lista de 23 problemas matemáticos compilados por el matemático alemán David Hilbert, presentados en el año 1900. Cabe anotar que originalmente Hilbert incluyó 24 problemas en su lista, pero decidió excluir uno de ellos de la publicada.
- La bomba Atomica cayo en Hiroshima a las 08:15 y 0+8+15=23
- El Titanic, se hundió el 15 de abril de 1912, lo curiosos es que si sumamos los dígitos de la fecha 15/04/1912; 1+5+0+4+1+9+1+2 = 23
- El World Trade Center (WTC), fue un complejo ubicado en Nueva York, Estados Unidos, donde se situaban las Torres Gemelas, destruidas el 11 de septiembre de 2001 a causa de un atentado terrorista. La fecha 11/09/2001 y 11+0+9+2+0+0+1 = 23
Fuentes:
CURIOSIDADES DEL 91
RETOS MATEMÁTICOSCuriosidades, Curiosidades de 91, Curiosidades matemáticas, Curiosidades numéricas
No hay comentarios

Si multiplicamos el número 91 por los números del 1 al 9, se obtienen unos resultados bien curiosos:





















.png)


.png)



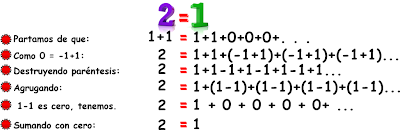



























.jpg)


