Los cuadrados mágicos son distribuciones de números en celdas que se disponen formando un cuadrado, de forma que la suma de cualquiera de las filas, de cualquiera de las columnas y de las dos diagonales principales da siempre el mismo resultado. Al número resultante se le denomina "constante o suma mágica".
El cuadrado mágico más pequeño es el que tiene 9 casillas, de orden 3 o de tamaño 3x3, Para iniciar puedes probar con los siguientes retos matemáticos en los que se pide que trasladen las tarjetas de tal manera que cada fila, cada columna y cada diagonal principal sume 15 :
HISTORIA
Se dice que el emperador de China Yü estaba en la orilla del río Amarillo cuando una tortuga salió de las aguas. Sobre su caparazón, la tortuga llevaba impresos extraños símbolos, que el emperador se encargó de descifrar. Eran los números del 1 al 9 dispuestos armoniosamente en forma de cuadrado: al sumar los tres números de cada fila, de cada columna o de cada diagonal el resultado era siempre el mismo.
Se dice que el emperador de China Yü estaba en la orilla del río Amarillo cuando una tortuga salió de las aguas. Sobre su caparazón, la tortuga llevaba impresos extraños símbolos, que el emperador se encargó de descifrar. Eran los números del 1 al 9 dispuestos armoniosamente en forma de cuadrado: al sumar los tres números de cada fila, de cada columna o de cada diagonal el resultado era siempre el mismo.
En China e India los cuadrados mágicos son conocidos desde antes de la era cristiana, pero en Europa se introdujeron durante el Renacimiento y llegaron a utilizarse como amuletos que llevaba la gente colgada de una chapa, pues se les atribuía poderes mágicos.
También se pueden encontrar cuadrados mágicos en el arte. El más famoso está incluido en un grabado de Alberto Durero, llamado Melancolía que se puede ver en el Germanisches National Museum de Nuremberg o en la Bibliothèque nationale de France, Paris.
En este grabado un robusto, ángel melancólico, obviamente atrapado en medio de una visión arquitectónica, con herramientas esparcidas y símbolos mágicos que la rodean, Durero pintó en lugar destacado un cuadrado mágico de orden 4.
El cuadrado mágico se puede observar en la parte superior derecha, debajo de una campana, está formado por los números del 1 al 16 y su constante o suma mágica es 34.
También podemos encontrar un cuadrado mágico en la fachada del templo de la Sagrada Familia, iniciado por el arquitecto Gaudí, en Barcelona.
A continuación vamos a mostrar cómo es nuestra propuesta pedagógica para integrar los cuadrados mágicos a una clase de matemáticas o para hacer de la misma una clase diferente, activa, participativa y dinámica.
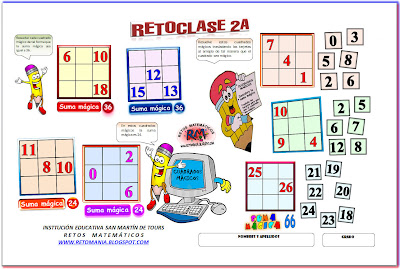
Retos Matemáticos inicia un ciclo de retos o desafíos matemáticos alusivos al fascinante mundo de los cuadrados mágicos, entretenimiento matemático muy antiguo y hoy todavía muy reconocido y divertido que permite el desarrollo de conceptos y muchas habilidades. Iniciamos con los cuadrados mágicos de orden 3 correspondiente al RetoClase No. 2A, publicado en marzo de 2013.
CUADRADO MÁGICO 1
Traemos dos cuadrados mágicos para que los estudiantes encuentren los números que hacen falta de tal manera que cada fila, columna y diagonal sea igual a 36.
CUADRADO MÁGICO 2
Resuelve estos dos cuadrados mágicos de tal manera que cada fila, columna y diagonal sea igual a 24.
CUADRADO MÁGICO 3
Presentamos tres cuadrados mágicos donde se presentan algunos de los números en el cuadrado y los estudiantes deben trasladar las tarjetas de tal manera que el cuadrado sea mágico.
Para todos aquellos docentes que quieren hacer una clase divertida o para todos aquellos amantes de la matemática pueden descargar todos estos desafíos matemáticos y pasar un rato bien ameno.
Puedes descargar la solución:
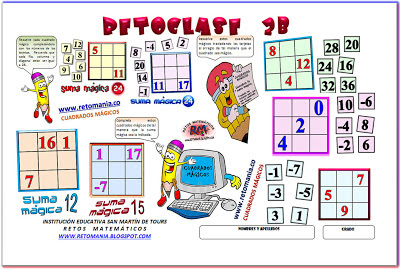
Retos Matemáticos continua con su ciclo de la temporada mágica, para esta semana traemos una serie de cuadrados mágicos en los que se busca que día a día encuentren todas las maravillas mágicas que ofrecen todos estos cuadrados. Presentamos variados cuadrados mágicos para resolver, recuerda que la suma de cada fila, cada columna y cada diagonal es la misma.
CUADRADO MÁGICO 1
Para resolver estos cuadrados mágicos, se deben trasladar las tarjetas al cuadrado para cumplir con la regla de oro: La suma de cada fila, columna y diagonal es la misma.
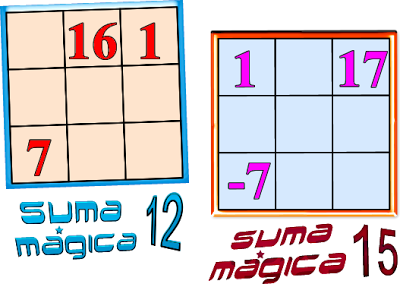
CUADRADO MÁGICO 2
Completar estos cuadrados mágicos con los números enteros que hacen falta de tal manera que la suma mágica sea la indicada:
CUADRADO MÁGICO 3
Resolver estos tres cuadrados mágicos trasladando las tarjetas al arreglo de tal manera que se cumpla con la regla mágica. Al sumar los números de cada fila, columna y diagonal, ésta es la misma.
Si te gusta la magia que encierran todos estos cuadrados, descarga e imprime todos estos desafíos matemáticos:
Descarga la solución:
Otros cuadrados mágicos que se presentaron durante este año 2013 son los siguientes:
- RetoClase 3A - Cuadrados Mágicos de Orden 3
- RetoClase 3B - Cuadrados Mágicos de Orden 3
- RetoClase 4A - Cuadrados Mágicos de Orden 4
- RetoClase 4B - Cuadrados Mágicos de Orden 4
CUADRADOS MÁGICOS
| |
 |  |
CUADRADOS MÁGICOS
| |
 |  |
CUADRADOS MÁGICOS
| |
 |  |
CUADRADOS MÁGICOS
| |
 |  |
CUADRADOS MÁGICOS
| |
 |  |
CUADRADOS MÁGICOS
| |
 |  |
CUADRADOS MÁGICOS
| |
 |  |
Y muchos más cuadrados mágicos ingresando a:
- Reto 20 - Cuadrados mágicos : Grados: 9°-10°-11°
- Reto 19 - Cuadrados mágicos: Grados: 10° - 11°
- Reto 17 - Cuadrados mágicos: Grados: 6° - 7°
- Reto 16 - Cuadrados mágicos: Grados: 8° - 9°
- Reto 10 - Cuadrados mágicos: Grados: 10° - 11°
- Reto 8 - Cuadrados mágicos: Grados: 6° - 7°
- Reto 7 - Cuadrados mágicos: Grados: 8° - 9°
.jpg)
