MULTIPLICACIÓN DIFERENTE

Como ya sabemos, la multiplicación es una operación matemática que consiste en sumar un número tantas veces como indica el otro número.  Así, 5x4 (cinco por cuatro), es igual a sumar cuatro veces el número 5, es decir:  5x4 = 5+5+5+5 = 20.  El resultado de la multiplicación recibe el nombre de producto y los números que se multiplican se llaman factores.

Si queremos multiplicar, 37 x 26, normalmente haríamos:

No son pocos los libros y sitios en internet donde se mencionan diferentes métodos de multiplicar.  Vamos a conocer algunos de éstos:

MÉTODO RUSO

Este método consiste en escribir los dos números A y B que se van a multiplicar en la parte superior como formando dos columnas.  

• Se inicia dividiendo el número A en dos, sucesivamente, ignorando el resto, hasta llegar a la unidad.
• A su vez, en la otra columna el número B se multiplica por 2 tantas veces como se ha dividido entre 2.  
• Se tachan todos los números pares de la primera columna y los correspondientes de la otra columna.
• Se suman todos los números de la segunda columna (no tachados).

Sigamos con el mismo ejemplo, multiplicar 37 x 26:

Observemos como este método sólo exige divisiones por 2 y duplicaciones, además de la suma final.

De hecho, hasta hace poco tiempo, a´si era que los campesinos de Rusia multiplicaban, y hay evidencias de uso reciente en Alemania, Francia e Inglaterra.  Por otro lados, es muy semejante al método empleado por los egipcios 20 siglos antes de la era cristiana.

MÉTODO EGIPCIO

El método utilizado en el antiguo Egipto sólo requiere saber sumar.  Si queremos multiplicar AxB, desarrollamos lo siguiente:

• Se forman dos columnas, en la primera columna escribimos la serie de números   2ⁿ, uno debajo de otro, es decir, 1, 2, 4, 8, 16 . . . ,  hasta que   2ⁿ,  sea menor o igual que el número A.
• En la segunda columna, se va escribiendo uno debajo de otro, el doble de cada número, empezando por el número B, hasta el último número de la primera columna.
• En la primera columna se marcan, puede ser con una x, los números cuya suma sea igual al número A.
• Sumamos los números correspondiente de la segunda columna a los marcados de la primera.  Este resultado es el producto de los números A y B.

Continuando con el primer ejemplo, multipliquemos 37x26

Si queremos multiplicar 45 x 32

Al multiplicamos 16 x 45, se presenta un caso especial, veamos:

MÉTODO  DE MULTIPLICACIÓN MAYA

Este método de multiplicación se basa en trazar tantas líneas como indique cada uno de los dígitos del número y luego se cuentan los puntos que quedan.  Veamos un ejemplo:  Multiplicar 12x23.  

• Lo primero que hay que hacer es de acuerdo al primer factor que es 12, trazar un línea correspondiente al primer dígito e inmediatamente después, dejando un espacio 2 líneas que corresponden al segundo dígito del primer factor.
• Se hace lo mismo con el segundo factor que 23, es decir se trazan 2 líneas correspondientes al primer dígito del factor y que se corten con las líneas anteriores y luego 3 líneas correspondientes al segundo dígito, como se observa en la figura:

Ahora se trazan dos arcos como se puede observar en la siguiente figura y procedemos a contar los puntos de cada área, así:

Observa:  Si se cuentan los puntos del área que cubre el primer arco, tenemos 2, luego contamos con del segundo arco y tenemos 6 y al contar los puntos centrales tenemos 7, por lo tanto el resultado es:  12x23=276.

Veamos un segundo ejemplo:  Multiplicar 31x22

No necesitamos calculadora, tampoco sabernos las tablas de multiplicar, sólo una hoja de papel, un lápiz, trazar rayas y por último contar puntos, así de fácil.

Y si la suma de los puntos es mayor o igual que 10 qué hacemos en este caso:  Multipliquemos 12x34.

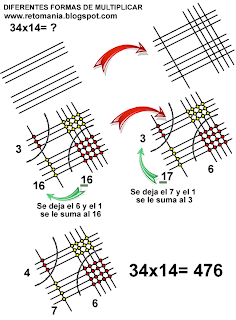
Hallemos ahora el producto de multiplicar 34x14.

Como respuesta a un interrogante por parte de un seguidor, publicamos la multiplicación 325x48.  Veamos:

Nos llegó un correo preguntando ¿como se aplicaría este proceso cuando uno o los dos números incluyen ceros?.  Veamos cómo multiplicar 105x302=?.

PRIMERO:  Se trazan las líneas de acuerdo a cada número.  ¿Pero cómo representar el cero?, pues bien trazamos 1  (una) línea como si fuera el número 1 pero con un color diferente.

SEGUNDO:  Marcamos los puntos donde hay cortes o intersecciones de las líneas.  No se tienen en cuenta los cortes donde interviene la línea de otro color (es el cero).

TERCERO:  Procedemos a contarlos, según los grupos, como se ilustra en la figura.

CUARTO:  Cuando se obtienen cantidades mayores que nueve, comenzamos de derecha a izquierda, dejando la cifra de las unidades y la de las decenas se la sumamos al resultado de la izquierda.  El resultado final se toma de todos los números que quedaron y se comienza ahora de derecha a izquierda.  Así 105x302=31710 tal como se puede comprobar efectuando la multiplicación.

Otra pregunta de nuestros seguidores:  ¿Cómo multiplicar 10x10? Veamos:

MULTIPLICACIÓN ARABE
Para este tipo de multiplicación, primero disponemos los números como se ilustra en la figura y elaboramos una tabla con tantas filas y columnas como dígitos tengan los factores.  Trazamos líneas dividiendo cada casilla de la tabla en dos.

Luego comenzamos a multiplicar el primer dígito del primer factor con el primer dígito del segundo factor, seguidamente el segundo dígito del primer factor con el primer dígito de segundo factor y así sucesivamente.   Las decenas se escriben en la parte superior de las casilla (dividida en 2) y las unidades en la inferior.   Observa el gráfico que ilustra mejor el procedimiento.  

Por último sumamos los números de cada diagonal comenzando de abajo hacia arriba.  Si la suma es mayor de diez, se deja o se escribe la unidad y se le suman a la siguiente diagonal.  El resultado final se forma juntando los números pero ahora de arriba abajo.

Veamos un segundo ejemplo donde la suma de los números de las casillas sea mayor que 10.